The Root-Locus Method¶
Given the following closed-loop controlled system:
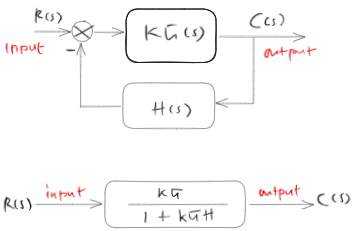
The root locus method draws the location of the closed-loop poles for all \(K \geq 0\).
However, the root-locus method does this by only considering the open-loop transfer function ( \(G(s)H(s)\) ).
Preparations¶
import numpy as np
from sympy import simplify, fraction, solve, expand, Symbol, re, im, Matrix, Eq, diff, latex
from sympy.physics.control.lti import TransferFunction
from sympy.abc import s
from rlocusanim import *
from mathprint import *
The core function for root-locus plotting¶
def rlocus(G, H, Kmax=10000, num=100):
K = Symbol('K', positive=True, real=True)
ol_tf = fraction(simplify(G * H));
ol_TF = TransferFunction(ol_tf[0], ol_tf[1], s)
ol_poles = np.complex64(ol_TF.poles())
ol_zeros = np.complex64(ol_TF.zeros())
cl_tf = fraction(simplify(K*G / (1+K*G*H)))
cl_TF = TransferFunction(cl_tf[0], cl_tf[1], s)
cl_poles = []
gains = np.logspace(np.log10(0.001), np.log10(Kmax), num)
gains = np.hstack((0, gains))
for gain in gains:
p = cl_TF.subs(K, gain).poles()
cl_poles.append([p[i].evalf() for i in range(len(p))])
cl_poles = np.complex64(cl_poles)
return gains, cl_poles, ol_poles, ol_zeros
Fiinding the \(j\omega\)-corssings¶
The crossings include: \(K\) and \(\omega\) at when the crossings occur.
def find_jw_crossings(G, H):
K = Symbol('K', positive=True, real=True)
omega = Symbol('omega', real=True)
cl_tf = fraction(simplify(K*G/(1+K*G*H)))
eq = cl_tf[1].subs(s, omega*1j)
# Build system equations made by real and immaginary compinents
eqs = Matrix([re(eq), im(eq)])
sol = solve(Eq(eqs,Matrix([[0],[0]])), [K,omega])
sol.insert(0, (K, omega))
mprint(latex(Matrix(sol)))
Finding break-away / entry points¶
Calculated from the characteristic function of the closed-loop-pole transfer function: \(\displaystyle 1 + KG(s) H(s) = 0\).
Express the closed-loop-pole transfer function as: \(K(s)=\dots\) (this should be a polynomial function of \(s\)-variable).
At break away / entry point,\(\displaystyle \frac{ \mathtt{d} K(s)}{ \mathtt{d} s} = 0\). Solve for \(s\). Assume the solutions are \(s=\mathcal{S}\).
To define if the point is valid: \(K(\mathcal{S}) > 0\).
To define whether the point is an entry point or a break-away point:
Entry point: \(\displaystyle \frac{ \mathtt{d}^2K(\mathcal{S})} { \mathtt{d} s^2} > 0\).
Break-away point: \(\displaystyle \frac{ \mathtt{d}^2K(\mathcal{S})}{ \mathtt{d} s^2} < 0\).
def find_break_entry_points(G, H):
K = Symbol('K', positive=True, real=True)
cl_tf = fraction(simplify(K*G/(1+K*G*H)))
eq = solve(cl_tf[1], K)[0]
deq = diff(eq, s)
ddeq = diff(eq, s, s)
sol = solve(deq, s)
sols = ([re(sol[i].evalf()) for i in range(len(sol))]) # this results should be only real numbers
S = []
for s_ in sols:
K_ = eq.subs(s, s_)
if K_ > 0:
S.append(s_)
STATUS = []
for s_ in S:
eq_ = ddeq.subs(s, s_)
if eq_.evalf() < 0:
STATUS.append("Break-away point")
else:
STATUS.append("Entry point")
return S, STATUS
Example 1¶
Rot-locus plot¶
%matplotlib notebook
gains, cl_poles, ol_poles, ol_zeros = rlocus(1/(s**3+s**2+45*s), 1, Kmax=2000);
ani = animate(gains, cl_poles, ol_poles, ol_zeros, gif_fn='./images/1.gif');
display_gif("./images/1.gif");
\(j \omega\)-crossings¶
find_jw_crossings(1/(s**3+s**2+45*s), 1)
Example 2¶
Root-locus plot¶
%matplotlib notebook
gains, cl_poles , ol_poles, ol_zeros = rlocus((s-1)/(s+3), 1)
ani = animate(gains, cl_poles, ol_poles, ol_zeros, gif_fn='./images/2.gif');
display_gif("./images/2.gif");
\(j \omega\)-crossings¶
find_jw_crossings((s-1)/(s+3), 1)
Example 3¶
Root-locus plot¶
%matplotlib notebook
gains, cl_poles , ol_poles, ol_zeros = rlocus(1/(s*(1+0.5*s)*(1+0.1*s)), 1, Kmax=200)
ani = animate(gains, cl_poles, ol_poles, ol_zeros, gif_fn='./images/3.gif', fps=60);
display_gif("./images/3.gif");
\(j \omega\)-crossings¶
find_jw_crossings(1/(s*(1+0.5*s)*(1+0.1*s)), 1)
For the shake of curiosity, let us do the calculation by hand.
Substitute \(\displaystyle s=j\omega \), and find the \(\displaystyle \omega \).
We can get two equations: \(\displaystyle -0.6\omega ^{2} +K=0\) and \(\displaystyle -0.05\omega ^{3} +\omega =0.\)
From: \(\displaystyle -0.05\omega ^{3} +\omega =0\Longrightarrow \cancel{\omega =0} \lor \omega =-4.472\lor \omega =4.472\).
\(\displaystyle \omega =0\) does not make any sense.
Take \(\displaystyle \omega =\pm 4.472\), substitute \(\displaystyle \omega \pm 4.472\) to \(\displaystyle -0.6\omega ^{2} +K=0\), and we get \(\displaystyle K=12\).
Break-away / entry points¶
S, STATUS = find_break_entry_points(1/(s*(1+0.5*s)*(1+0.1*s)), 1)
print(S)
print(STATUS)
[-0.944949536696107]
['Break-away point']
Example 4¶
To get a nice root-locus plot, we need to play a bit with the Kmax and num arguments. Otherwise, our root-locus plot will look funny.
Root-locus plot¶
%matplotlib notebook
gains, cl_poles , ol_poles, ol_zeros = rlocus((s+2)*(s+3)/(s*(s+1)), 1, Kmax=100, num=1000)
ani = animate(gains, cl_poles, ol_poles, ol_zeros, gif_fn='./images/4.gif', fps=500);
display_gif("./images/4.gif");
Break-away / entry points¶
S, STATUS = find_break_entry_points((s+2)*(s+3)/(s*(s+1)), 1)
print(S)
print(STATUS)
[-2.36602540378444, -0.633974596215561]
['Entry point', 'Break-away point']
