kalman-cpp

Kalman Filter for Linear Systems

Definition

A linear system is described as follows.

\[x_k = Ax_{k-1} + Bu_{k-1} + v_{k-1}\]

\[z_k = Hx_k + w_k\]

where:
\(v\) is the process noise (Gaussian with covariance Q)

\(w\) is the measurement noise (Gaussian with covariance R)
\(A\) is the system matrix
\(B\) is the input matrix
\(H\) is the output matrix
\(x\) is the state vector
\(z\) is the output vector
\(u\) is the input vector

The noise covariance matrices must follow these conditions:

\[Q = Q^T\]

\[R = R^T\]

Examples

<<<<<<< HEAD

An example is provided in main1.cpp solves the car voltmeter problem using this library. The system model for this problem is governed by:
=======

An example provided in main1.cpp solvesthe car voltmeter problem using this library. The system model for this problem is governed by:
>>>>>>> c467bb8b4126460c1e18ba28ee4392f49fdc6552

\[x_k = 12 + v_{k-1}\]

\[z_k = x_k + w_ḳ\]

Let us extract the model parameters from the equation above: \(A = 0\), \(B = 1\), \(H = 1\), \(u = 12\), \(x_0 = 12\), \(Q=4\), and \(R=4\). Now that we know all the parameter values, we can then set up the following piece of code:

mat A(1,1), B(1,1), H(1,1), Q(1,1), R(1,1);
colvec u(1);  
 
A << 0;
B << 1;
Q << 4;
H << 1;
R << 4;
u << 12.0;

The first and second line of the code above are used to create all the necessary matrices with correct dimensions. In the following lines, we apply the correct value for each matrix.

Our next step is to create an instance of class class and initialize it with the previously created \(A\), \(B\), \(Q\), \(H\), and \(R\) matrices.

KF kalman;
kalman.InitSystem(A, B, H, Q, R);

And or our last step, we run the Kalman procedure repetitively as shown in the code below.

for (int k = 0; k < 100; k++) {
  kalman.Kalmanf(u);
  
  // The rest of the code 
}

Extended Kalman Filter (EKF) for nonlinear systems

Definition

A non-linear system is described by:

\[x_k = f(x_{k-1}, u_{k-1}) + v_{k-1}\]

\[z_k = h(x_k) + w_k\]

where:
\(f\) is the dynamic model of the system
\(h\) is the measurement model of the system
\(v\) is the process noise (Gaussian with covariance Q)

\(w\) is the measurement noise (Gaussian with covariance R)
\(x\) is the state vector
\(z\) is the output vector
\(u\) is the input vector

The noise covariance matrices must follow these conditions:

\[Q = Q^T\]

\[R = R^T\]

Example

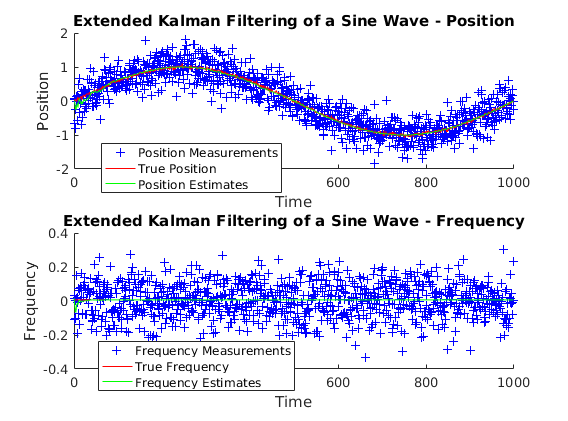
Here, let us take main4.cpp as an example. This content of this file is adapted from this
MATLAB Central page.

Let us define a nonlinear system as follows.

\[ f = \begin{bmatrix} \sin(x_2(k-1))(k-1) \\ x_2(k-1) \end{bmatrix} \]

\[ h = \begin{bmatrix} x_1(k) \\ x_2(k) \end{bmatrix} \]

\[ x_0 = \begin{bmatrix} 0 \\ \frac{1 \pi}{500} \end{bmatrix}\]

A nonlinear function does not have a strict tempate as in a linear function. Therefore, we need to let the user to derive the EKF class for flexible implementation of a nonlinear model for both the process and the the measurement.

class MyEKF: public EKF
{
public:  
  virtual colvec f(const colvec& x, const colvec& u) {
    colvec xk(nOutputs_);
    xk(0) = sin(x(1) * u(0));
    xk(1) = x(1);
    return xk;
  }
  
  virtual colvec h(const colvec& x) {
    colvec zk(nOutputs_);
    zk(0) = x(0);
    zk(1) = x(1);
    return zk;
  }
};

The next steps below are very similiar to the previous example in the linear Kalman filter section. First, we start by creating all necessary matrices and set their values accordingly. Afterward, we continue with initializing. the covariance matrices as well as the state vector. In the final step, we run the EKF procedurerepetitively while logging necessary data.

int main(int argc, char** argv)
{
   //
   // Log the result into a tab delimitted file, later we can open 
   // it with Matlab. Use: plot_data4.m to plot the results.
   //
  ofstream log_file;
  log_file.open("log_file4.txt");
  
  int n_states = 2;
  int n_outputs = 2;
  mat Q(2, 2);
  mat R(2, 2);
  
  Q << 0.001 << 0    << endr
    << 0     << 0    << endr;
    
  R << 0.1   << 0    << endr
    <<   0   << 0.01 << endr;
  
  colvec x0(2);
  x0 << 0 << 1 * M_PI / 500;
  
  colvec u(1);
   
  MyEKF myekf;
  myekf.InitSystem(n_states, n_outputs, Q, R);
  myekf.InitSystemState(x0);
  
  for (int k = 0; k < 1000; k ++) {
    u(0) = k;
    myekf.EKalmanf(u);
    
    colvec *x = myekf.GetCurrentState();
    colvec *x_m = myekf.GetCurrentEstimatedState();
    colvec *z = myekf.GetCurrentOutput();
    
    log_file << k 
             << '\t' << z->at(0,0) << '\t' << x->at(0,0) << '\t' << x_m->at(0,0)
             << '\t' << z->at(1,0) << '\t' << x->at(1,0) << '\t' << x_m->at(1,0)
             << '\n'; 
  }
  
  log_file.close();
  
  return 0;
}

Unscented Kalman Filter (UKF) for a nonlinear system

Another type of Kalman Filter for a nonlinear system is the Unscented Kalman Filter. It addresses the accuracy problem which arises during linearization process of an Extended Kalman filter when Jacobian is used. The Unscented Kalman Filter is implemented in class UKF and the steps for using the provided UKF class is exactly similiar as in using the EKF class.

The implementation of the UKF in this C++ library is based on the following paper:

Wan, E. A., & Van Der Merwe, R. (2006). The unscented Kalman filter for nonlinear estimation. Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), 31(2), 153–158.

The paper above can be downloaded from here.

Example

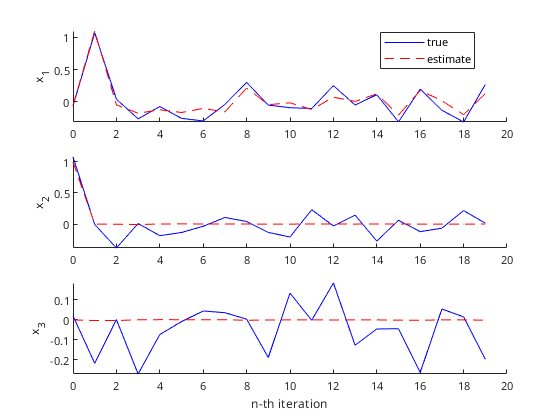
Here, we take main10.cpp as an example. This example is adapted from this

This example is taken fromhere. The nonlinear system is described as follows.

\[ f = \begin{bmatrix} x_2(k) \\ x_3(k) \\ 0.005 \, x_1(k) \bigg(x_2(k) + x_3(k) \bigg) \end{bmatrix} \]

\[ h = \begin{bmatrix} x_1(k) \end{bmatrix} \]

\[ x_0 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]

The following lines of codes show how to use the UKF class. As mentioned before, we need to first derive the UKF class and define the virtual functions f (process function) and h (output function).

class MyUKF : public UKF
{
public:
    virtual colvec f(const colvec& x, const colvec& u) {
        colvec xk(nStates_);
        xk.at(0) = x(1);
        xk.at(1) = x(2);
        xk.at(2) = 0.05*x(0)*(x(1)+x(2));
        return xk;
    }
 
    virtual colvec h(const colvec& x) {
        colvec zk(nOutputs_);
        zk(0) = x(0);
        return zk;
    }
};
 
 
int main(int argc, char** argv)
{
    mat Q(3, 3);
    mat R(1, 1);
 
 
    MyUKF myukf;
 
    double r = 0.1;
    double q = 0.1;
    
    Q = eye(3,3)*q*q;
    R << r*r << endr;
 
    colvec x0(3);
    x0 << 0 << 0 << 1;
 
    mat P0 = eye<mat>(3, 3);
    P0 =  P0;
 
    colvec u;
 
    // No inputs
    u = u.zeros();
 
    myukf.InitSystem(3, 1, Q, R);
    myukf.InitSystemState(x0);
    myukf.InitSystemStateCovariance(P0);
 
    for (int k = 0; k < 20; k++) {
        myukf.UKalmanf(u);
 
        colvec *x = myukf.GetCurrentState();
        colvec *x_m = myukf.GetCurrentEstimatedState();
        colvec *z = myukf.GetCurrentOutput();
        colvec *z_m = myukf.GetCurrentEstimatedOutput();
    }
 
    return 0;
}

These are the plots that show comparisons between measurements and estimations of the three states: \(x_1\), \(x_2\) and \(x_3\).

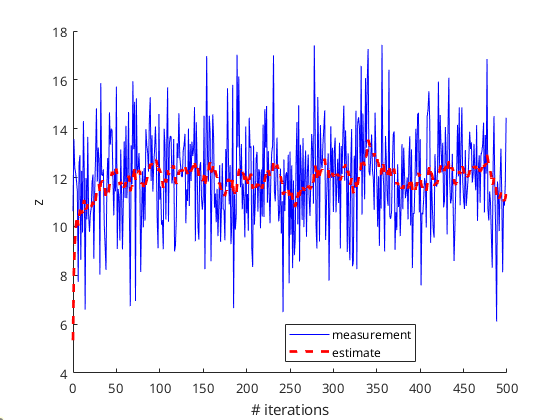
Practical application: Kalman filter for noisy measurements

The examples we have so far are theoretical. Very often, what we would like to do is to reduce noise from pre-acquired measurement data. There are several reasons why we want to use Kalman filter. For example, noise has a vast spectrum. Thus, using a frequency-based filter hurts the data.

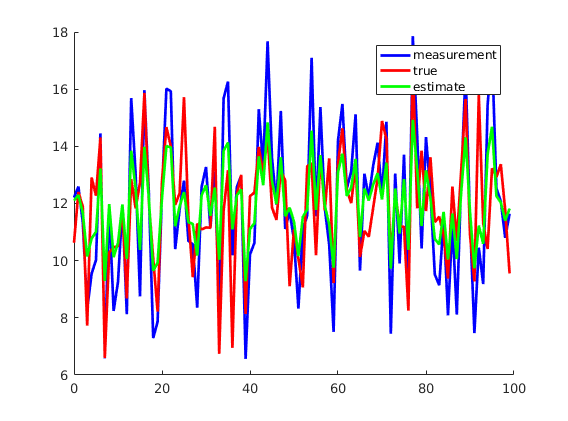
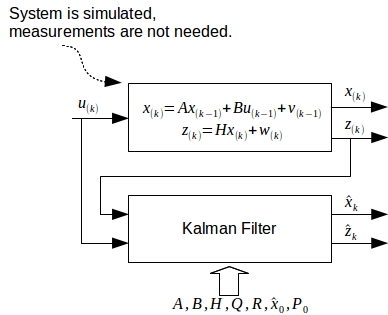
Principally, there are two scenarios of using the Kalman filtering techniquie here. The first scenario is by first simulating the system, as shown in the figure below.

In this scenario, we only need to supply \(u_k\) to the Kalman filter function. The Kalman procedure will give us four outputs as a result: \(x_k\), \(z_k\), \(\hat{x}_k\), and \(\hat{z}_k\). \(x_k\) and \(z_k\) are called the true states and the true outputs, respectvely. They are noisy. \(\hat{x}_k\), and \(\hat{z}_k\) are called the estimated states and the estimated outputs, respectively. They are filtered, look smoother and closer to the noiseless true states.

The function prototype for the scenario above can be written as:
[ \(x_k\), \(z_k\), \(\hat{x}_k\), \(\hat{z}_k\)] = function kalmanf( \(u_k\))

The second scenario is used when the measurements are available. Thus, simulating the system becomes unnecessary. In such a scenario, we need to supply both \(z_k\) and \(u_k\) to the kalman filter function. The Kalman filter will give us 2 outputs: \(\hat{x}_k\) (the estimated system sates) and \(\hat{z}_k\) (the estimated system outputs).

The function prototype for this scenario can be written as:
[ \(\hat{x}_k\), \(\hat{z}_k\)] = function kalmanf( \(z_k\), \(u_k\))

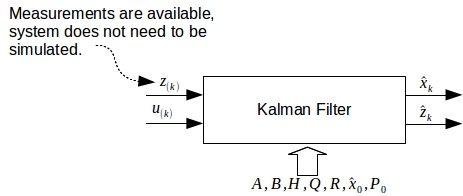
The second scenario is useful for smoothing noisy measurment data. However, both scenarios are availabe in this library.

Example

As one example, let us see the problem provided in main1.cpp. This time, however, we assume we have already had several noisy data points from measurements. Therfore, we will not need the Kalman procedure to simulate the system.
The system model can be formulated into:

\[x_k = x_{k-1} + v_{k-1}\]

\[z_k = x_k + w_ḳ\]

We then generate random number as the prerecorded noisy data (z_measurement), as follows.

// Assume we have a noisy signal that is acquired from a measurement tool
double w = 2; // Stdev of the noise, in reality we don't know this
colvec z_measurement(1);
z_measurement.randn(1);
z_measurement = z_measurement * w + 12.0;

After than, z_measurement is sent to the Kalman filter function, as the following:

// Put the z_measurment to the Kalman filter
kalman.Kalmanf(z_measurement, u);
 
colvec *z_m = kalman.GetCurrentEstimatedOutput();
colvec *x_m = kalman.GetCurrentEstimatedState();

The kalman.Kalmanf(z_measurement, u) function above has different parameters with what we can find in main1.cpp. Since z_measurement is available, we then send it as a parameter for the kalmanf function. The processes above are done in several iterations according to the number of the availabe data points. The final codes will look like as the following:

int main(int argc, char** argv)
{      
  // Log the result into a tab delimitted file, later we can open 
  // it with Matlab. Use: plot_data7.m to plot the results.
  
  ofstream log_file;
  log_file.open("log_file7.txt");
  
  // Define the system and initialize the Kalman filter
   
  mat A(1,1), B(1,1), H(1,1), Q(1,1), R(1,1);
  colvec u(1);
  colvec x0(1);  
    
  A << 1;
  B << 1;
  Q << 0.01; // Heuristic tuning parameter
  H << 1;
  R << 1;    // Heuristic tuning parameter
  u << 0;
    
  KF kalman;
  kalman.InitSystem(A, B, H, Q, R);
    
  int N = 500;
  
  for (int k = 0; k < N; k++) {
        
    // Assume we have a noisy signal that is acquired from a measurement tool
    double w = 2; // Stdev of the noise, in reality we don't know this
    colvec z_measurement(1);
    z_measurement.randn(1);
    z_measurement = z_measurement * w + 12.0;
      
    // Put the z_measurment to the Kalman filter
    kalman.Kalmanf(z_measurement, u);
      
    colvec *z_m = kalman.GetCurrentEstimatedOutput();
    colvec *x_m = kalman.GetCurrentEstimatedState();
     
    log_file << k << '\t' << z_measurement.at(0,0) << '\t' << z_m->at(0,0)  
             << '\n'; 
  }
  return 0;
}

The values that are given to Q and R are defined heuristically since we do not know the actual variances of the noise of the data.