Digital PID Control - Part 2

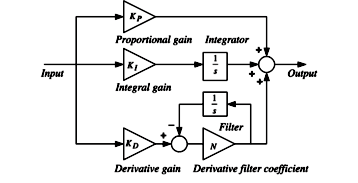
In this section, we will – part-by-part – derive the integral and derivative terms of a PID control. We will use backward Euler, forward Euler, and bilinear transformation for the discretization.

Required Imports

from IPython.core.display import HTML
from sympy import *
from mathprint import *

Preparations

Kp, Ki, Kd = symbols('K_p K_i K_d', positive=True)

Ts, N = symbols('T_s N', positive=True)
t  = symbols('t', positive=True)
s  = symbols('s', complex=True)
z  = symbols('z')

e, P, I, D = symbols('e P I D')
e1p, e0, e1, e2 = symbols('e_{k+1} e_k e_{k-1} e_{k-2}')
I1p, I0, I1, I2 = symbols('I_{k+1} I_k I_{k-1} I_{k-2}')
D1p, D0, D1, D2 = symbols('D_{k+1} D_k D_{k-1} D_{k-2}')

The Three Transformations

• FE for Forward Euler (ZOH)

• BE for Backward Euler (ZOH)

• BT for Bilinear Transformation (Tustin)

FE = Ts / (z- 1)
BE = z*Ts / (z-1)
BT = Ts/2 * (z+1)/(z-1)

Integral Control Action

Let us set \(G_I\) as the integral control transfer funcion and \(K_i\) as the gain.

GI = Ki/s
mprint("G_I(s)= ", latex(GI))

\[\displaystyle G_I(s)= \frac{K_{i}}{s}\]

With Backward Euler

Let us set \(e\) as the control input and \(I\) as the control output.

eq = Eq(I, e*GI.subs(1/s, BE))
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs, eq.rhs))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e*z, e1p).subs(e, e0).subs(I/z, I1).subs(I*z, I1p).subs(I, I0)
mprint(latex(eq))

IBE = Eq(collect(eq.rhs, [1/Ts]), collect(eq.lhs, [Ki]) )
mprint(latex(IBE))

IBE = Eq(I1p, solve(IBE, I1p)[0])
mprintb(latex(IBE))

\[\displaystyle I = \frac{K_{i} T_{s} e z}{z - 1}\]

\[\displaystyle K_{i} T_{s} e z = I \left(z - 1\right)\]

\[\displaystyle K_{i} T_{s} e z = I z - I\]

\[\displaystyle K_{i} T_{s} e_{k+1} = - I_{k} + I_{k+1}\]

\[\displaystyle - I_{k} + I_{k+1} = K_{i} T_{s} e_{k+1}\]

\[\displaystyle \boxed{I_{k+1} = I_{k} + K_{i} T_{s} e_{k+1}}\]

With Forward Euler

Let us set \(e\) as the control input and \(I\) as the control output.

eq = Eq(I, e*GI.subs(1/s, FE))
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs, eq.rhs ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e*z, e1p).subs(e, e0).subs(I/z, I1).subs(I*z, I1p).subs(I, I0)
mprint(latex(eq))

IFE = Eq(collect(eq.rhs, [1/Ts]), collect(eq.lhs, [Ki]) )
mprint(latex(IFE))

IFE = Eq(I1p, solve(IFE, I1p)[0])
mprintb(latex(IFE))

\[\displaystyle I = \frac{K_{i} T_{s} e}{z - 1}\]

\[\displaystyle K_{i} T_{s} e = I \left(z - 1\right)\]

\[\displaystyle K_{i} T_{s} e = I z - I\]

\[\displaystyle K_{i} T_{s} e_{k} = - I_{k} + I_{k+1}\]

\[\displaystyle - I_{k} + I_{k+1} = K_{i} T_{s} e_{k}\]

\[\displaystyle \boxed{I_{k+1} = I_{k} + K_{i} T_{s} e_{k}}\]

With Bilinear Transformation

Let us set \(e\) as the control input and \(I\) as the control output.

eq = Eq(I, e*GI.subs(1/s, BT))
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/Ts, eq.rhs/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e*z, e1p).subs(e, e0).subs(I/z, I1).subs(I*z, I1p).subs(I, I0)
mprint(latex(eq))

IBT = Eq(I1p, solve(eq, I1p)[0])
mprint(latex(IBT))

IBT = Eq(I1p, collect(IBT.rhs, Ki*Ts/2))
mprintb(latex(IBT))

\[\displaystyle I = \frac{K_{i} T_{s} e \left(z + 1\right)}{2 \left(z - 1\right)}\]

\[\displaystyle K_{i} T_{s} e \left(z + 1\right) = I \left(2 z - 2\right)\]

\[\displaystyle K_{i} e z + K_{i} e = \frac{2 I z}{T_{s}} - \frac{2 I}{T_{s}}\]

\[\displaystyle K_{i} e_{k} + K_{i} e_{k+1} = - \frac{2 I_{k}}{T_{s}} + \frac{2 I_{k+1}}{T_{s}}\]

\[\displaystyle I_{k+1} = I_{k} + \frac{K_{i} T_{s} e_{k}}{2} + \frac{K_{i} T_{s} e_{k+1}}{2}\]

\[\displaystyle \boxed{I_{k+1} = I_{k} + \frac{K_{i} T_{s} \left(e_{k} + e_{k+1}\right)}{2}}\]

Differential Control Action

Let us set \(G_D\) as the integral control transfer funcion and \(K_d\) as the gain.

GD = s*Kd
mprint("G_D(s)= ", latex(GD))

\[\displaystyle G_D(s)= K_{d} s\]

With Backward Euler

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GD.subs(1/s, BE))
mprint(latex(eq))

eq = factor(eq)
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/z/Ts, eq.rhs/z/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e, e0).subs(D/z, D1).subs(D, D0)
mprint(latex(eq))

DBE = Eq(collect(eq.rhs, [D0, D1]), collect(eq.lhs, Kd/Ts))
mprintb(latex(DBE))

\[\displaystyle D = \frac{K_{d} e \left(z - 1\right)}{T_{s} z}\]

\[\displaystyle D = \frac{K_{d} e \left(z - 1\right)}{T_{s} z}\]

\[\displaystyle K_{d} e \left(z - 1\right) = D T_{s} z\]

\[\displaystyle \frac{K_{d} e}{T_{s}} - \frac{K_{d} e}{T_{s} z} = D\]

\[\displaystyle \frac{K_{d} e_{k}}{T_{s}} - \frac{K_{d} e_{k-1}}{T_{s}} = D_{k}\]

\[\displaystyle \boxed{D_{k} = \frac{K_{d} \left(e_{k} - e_{k-1}\right)}{T_{s}}}\]

With Forward Euler

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GD.subs(1/s, FE))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e*z, e1p).subs(e, e0).subs(D/z, D1).subs(D, D0)
mprint(latex(eq))

DFE = Eq(eq.lhs, collect(eq.rhs, Kd/Ts))
mprintb(latex(DFE))

\[\displaystyle D = \frac{K_{d} e \left(z - 1\right)}{T_{s}}\]

\[\displaystyle D_{k} = - \frac{K_{d} e_{k}}{T_{s}} + \frac{K_{d} e_{k+1}}{T_{s}}\]

\[\displaystyle \boxed{D_{k} = \frac{K_{d} \left(- e_{k} + e_{k+1}\right)}{T_{s}}}\]

With Bilinear Transformation

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GD.subs(1/s, BT))
mprint(latex(eq))

eq = factor(eq)
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/z/Ts, eq.rhs/z/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e, e0).subs(D/z, D1).subs(D, D0)
mprint(latex(eq))

DBT = Eq(D0, solve(eq, D0)[0])
mprint(latex(DBT))

DBT = Eq(D0, collect(DBT.rhs, 2*Kd))
mprintb(latex(DBT))

\[\displaystyle D = \frac{2 K_{d} e \left(z - 1\right)}{T_{s} \left(z + 1\right)}\]

\[\displaystyle D = \frac{2 K_{d} e \left(z - 1\right)}{T_{s} \left(z + 1\right)}\]

\[\displaystyle 2 K_{d} e \left(z - 1\right) = D T_{s} \left(z + 1\right)\]

\[\displaystyle \frac{2 K_{d} e}{T_{s}} - \frac{2 K_{d} e}{T_{s} z} = D + \frac{D}{z}\]

\[\displaystyle \frac{2 K_{d} e_{k}}{T_{s}} - \frac{2 K_{d} e_{k-1}}{T_{s}} = D_{k} + D_{k-1}\]

\[\displaystyle D_{k} = \frac{- D_{k-1} T_{s} + 2 K_{d} e_{k} - 2 K_{d} e_{k-1}}{T_{s}}\]

\[\displaystyle \boxed{D_{k} = \frac{- D_{k-1} T_{s} + 2 K_{d} \left(e_{k} - e_{k-1}\right)}{T_{s}}}\]

Differential Control Action with Derivative Filter

Let us set \(G_D\) as the integral control transfer funcion, \(K_d\) as the gain and \(1/N\) as the filter time-constant.

GDF = s*Kd*1/(1/N*s+1)
mprint("G_D(s)= ", latex(GD))

GDF = simplify(GDF)
mprint("G_D(s)= ", latex(GD))

\[\displaystyle G_D(s)= K_{d} s\]

\[\displaystyle G_D(s)= K_{d} s\]

With Backward Euler

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GDF.subs(1/s, BE))
mprint(latex(eq))

eq = factor(eq)
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/z/Ts, eq.rhs/z/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e, e0).subs(D/z, D1).subs(D, D0)
mprint(latex(eq))

DBEF = Eq(collect(eq.rhs, [D0, D1]), collect(eq.lhs, N*Kd/Ts))
mprint(latex(DBEF))

DBEF = Eq(D0, collect(solve(DBEF, D0)[0], Kd*N))
mprintb(latex(DBEF))

\[\displaystyle D = \frac{K_{d} N e \left(z - 1\right)}{T_{s} z \left(N + \frac{z - 1}{T_{s} z}\right)}\]

\[\displaystyle D = \frac{K_{d} N e \left(z - 1\right)}{N T_{s} z + z - 1}\]

\[\displaystyle K_{d} N e \left(z - 1\right) = D \left(N T_{s} z + z - 1\right)\]

\[\displaystyle \frac{K_{d} N e}{T_{s}} - \frac{K_{d} N e}{T_{s} z} = D N + \frac{D}{T_{s}} - \frac{D}{T_{s} z}\]

\[\displaystyle \frac{K_{d} N e_{k}}{T_{s}} - \frac{K_{d} N e_{k-1}}{T_{s}} = D_{k} N + \frac{D_{k}}{T_{s}} - \frac{D_{k-1}}{T_{s}}\]

\[\displaystyle D_{k} \left(N + \frac{1}{T_{s}}\right) - \frac{D_{k-1}}{T_{s}} = \frac{K_{d} N \left(e_{k} - e_{k-1}\right)}{T_{s}}\]

\[\displaystyle \boxed{D_{k} = \frac{D_{k-1} + K_{d} N \left(e_{k} - e_{k-1}\right)}{N T_{s} + 1}}\]

With Forward Euler

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GDF.subs(1/s, FE))
mprint(latex(eq))

eq = factor(eq)
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/Ts, eq.rhs/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e*z, e1p).subs(e, e0).subs(D/z, D1).subs(D*z, D1p).subs(D, D0)
mprint(latex(eq))

DFEF = Eq(collect(eq.rhs, [D0, D1]), collect(eq.lhs, Kd*N/Ts))
mprint(latex(DFEF))

DFEF = Eq(D0, collect(solve(DFEF, D0)[0], [Kd*N, D1]))
mprintb(latex(DFEF))

\[\displaystyle D = \frac{K_{d} N e \left(z - 1\right)}{T_{s} \left(N + \frac{z - 1}{T_{s}}\right)}\]

\[\displaystyle D = \frac{K_{d} N e \left(z - 1\right)}{N T_{s} + z - 1}\]

\[\displaystyle K_{d} N e \left(z - 1\right) = D \left(N T_{s} + z - 1\right)\]

\[\displaystyle \frac{K_{d} N e z}{T_{s}} - \frac{K_{d} N e}{T_{s}} = D N + \frac{D z}{T_{s}} - \frac{D}{T_{s}}\]

\[\displaystyle - \frac{K_{d} N e_{k}}{T_{s}} + \frac{K_{d} N e_{k+1}}{T_{s}} = D_{k} N - \frac{D_{k}}{T_{s}} + \frac{D_{k+1}}{T_{s}}\]

\[\displaystyle D_{k} \left(N - \frac{1}{T_{s}}\right) + \frac{D_{k+1}}{T_{s}} = \frac{K_{d} N \left(- e_{k} + e_{k+1}\right)}{T_{s}}\]

\[\displaystyle \boxed{D_{k} = \frac{- D_{k+1} + K_{d} N \left(- e_{k} + e_{k+1}\right)}{N T_{s} - 1}}\]

With Bilinear Transformation

Let us set \(e\) as the control input and \(D\) as the control output.

eq = Eq(D, e*GDF.subs(1/s, BT))
mprint(latex(eq))

eq = factor(eq)
mprint(latex(eq))

eq = (Eq(numer(eq.rhs), eq.lhs * denom(eq.rhs)))
mprint(latex(eq))

eq = expand(Eq(eq.lhs/z/Ts, eq.rhs/z/Ts ))
mprint(latex(eq))

eq = expand(eq).subs(e/z**2, e2).subs(e/z, e1).subs(e, e0).subs(D/z, D1).subs(D, D0)
mprint(latex(eq))

DBTF = Eq(D0, collect(solve(eq, D0)[0], [2*Kd*N, D1]))
mprintb(latex(DBTF))

\[\displaystyle D = \frac{2 K_{d} N e \left(z - 1\right)}{T_{s} \left(N + \frac{2 \left(z - 1\right)}{T_{s} \left(z + 1\right)}\right) \left(z + 1\right)}\]

\[\displaystyle D = \frac{2 K_{d} N e \left(z - 1\right)}{N T_{s} z + N T_{s} + 2 z - 2}\]

\[\displaystyle 2 K_{d} N e \left(z - 1\right) = D \left(N T_{s} z + N T_{s} + 2 z - 2\right)\]

\[\displaystyle \frac{2 K_{d} N e}{T_{s}} - \frac{2 K_{d} N e}{T_{s} z} = D N + \frac{D N}{z} + \frac{2 D}{T_{s}} - \frac{2 D}{T_{s} z}\]

\[\displaystyle \frac{2 K_{d} N e_{k}}{T_{s}} - \frac{2 K_{d} N e_{k-1}}{T_{s}} = D_{k} N + \frac{2 D_{k}}{T_{s}} + D_{k-1} N - \frac{2 D_{k-1}}{T_{s}}\]

\[\displaystyle \boxed{D_{k} = \frac{D_{k-1} \left(- N T_{s} + 2\right) + 2 K_{d} N \left(e_{k} - e_{k-1}\right)}{N T_{s} + 2}}\]

Summary

Integral Terms

Let us summarize the integral terms. Note that the backward Euler method and the bilinear transform method result in implicit-form equations.

Show code cell source Hide code cell source

from pandas import DataFrame
from IPython.display import Markdown

def makelatex(args):
    return ["${}$".format(latex(a)) for a in args]
    
descs = ["Backward Euler", 
         "Forward Euler",
         "Bilinear Transform"]

vals  = [IBE, IFE, IBT]

dic = {'Method': descs, 
       'Integral term': makelatex(vals),}

df = DataFrame(dic)
Markdown(df.to_markdown(index=False))

Method	Integral term
Backward Euler	\(I_{k+1} = I_{k} + K_{i} T_{s} e_{k+1}\)
Forward Euler	\(I_{k+1} = I_{k} + K_{i} T_{s} e_{k}\)
Bilinear Transform	\(I_{k+1} = I_{k} + \frac{K_{i} T_{s} \left(e_{k} + e_{k+1}\right)}{2}\)

Derivative Terms

Let us summarize the derivative terms. Note that forward Euler results in non-causal equation.

Show code cell source Hide code cell source

descs = ["Backward Euler", 
         "Forward Euler",
         "Bilinear Transform"]

vals  = [DBE, DFE, DBT]

dic = {'Method': descs, 
       'Derivative term': makelatex(vals),}

df = DataFrame(dic)
Markdown(df.to_markdown(index=False))

Method	Derivative term
Backward Euler	\(D_{k} = \frac{K_{d} \left(e_{k} - e_{k-1}\right)}{T_{s}}\)
Forward Euler	\(D_{k} = \frac{K_{d} \left(- e_{k} + e_{k+1}\right)}{T_{s}}\)
Bilinear Transform	\(D_{k} = \frac{- D_{k-1} T_{s} + 2 K_{d} \left(e_{k} - e_{k-1}\right)}{T_{s}}\)

Derivative Terms with Low-Pass Filters

Let us summarize the filtered derivative terms. Note that forward Euler also results in non-causal equation.

Show code cell source Hide code cell source

descs = ["Backward Euler", 
         "Forward Euler",
         "Bilinear Transform"]

vals  = [DBEF, DFEF, DBTF]

dic = {'Method': descs, 
       'Derivative term + low-pass filter': makelatex(vals),}

df = DataFrame(dic)
Markdown(df.to_markdown(index=False))

Method	Derivative term + low-pass filter
Backward Euler	\(D_{k} = \frac{D_{k-1} + K_{d} N \left(e_{k} - e_{k-1}\right)}{N T_{s} + 1}\)
Forward Euler	\(D_{k} = \frac{- D_{k+1} + K_{d} N \left(- e_{k} + e_{k+1}\right)}{N T_{s} - 1}\)
Bilinear Transform	\(D_{k} = \frac{D_{k-1} \left(- N T_{s} + 2\right) + 2 K_{d} N \left(e_{k} - e_{k-1}\right)}{N T_{s} + 2}\)