Two-Layer Fully Connected Neural Network¶
This material is heavily based on the popular Standford CS231n lecture material. Please check on their website for more detailed information.
Preparations¶
As usual, let’s start with some preparations.
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
plt.rcParams.update({
"text.usetex": True,
"font.family": "sans-serif",
"font.size": 10,
})
from utils import *
np.set_printoptions(precision=5, suppress=True)
Diagram of the neural network¶
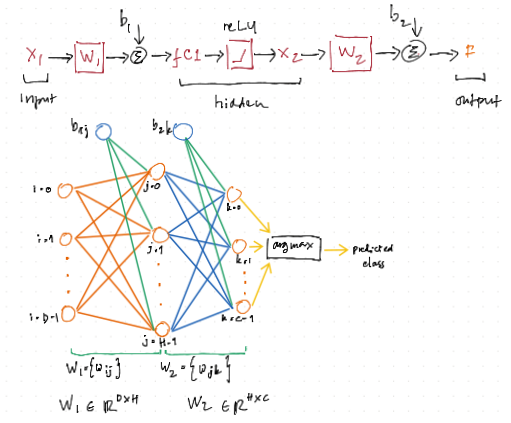
class TwoLayerNet¶
Here, we are using the the ScyPy instead of our previous gradient descent method. There are: D*H+H*C+H+C variables that we must solve. For this reasons, our vanilla gradient descent method often gives unsatisfactory results.
class TwoLayerNet():
"""
A two-layer fully-connected neural network. The net has an input dimension of
N, a hidden layer dimension of H, and performs classification over C classes.
We train the network with a softmax loss function and L2 regularization on the
weight matrices. The network uses a ReLU nonlinearity after the first fully
connected layer.
In other words, the network has the following architecture:
input - fully connected layer - ReLU - fully connected layer - softmax
The outputs of the second fully-connected layer are the scores for each class.
"""
def __init__(self, input_size, hidden_size, output_size, std=1e-5):
"""
Initialize the model. Weights are initialized to small random values and
biases are initialized to zero. Weights and biases are stored in the
variable self.params, which is a dictionary with the following keys:
W1: First layer weights; has shape (D, H)
b1: First layer biases; has shape (H,)
W2: Second layer weights; has shape (H, C)
b2: Second layer biases; has shape (C,)
Inputs:
- input_size: The dimension D of the input data.
- hidden_size: The number of neurons H in the hidden layer.
- output_size: The number of classes C.
"""
self.params = {}
self.params['W1'] = std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
@staticmethod
def loss(W1, b1, W2, b2, X, Y, reg, grad=False):
"""
Compute the loss and gradients for a two layer fully connected neural
network.
Inputs:
- X: Input data of shape (N, D). Each X[i] is a training sample.
- Y: Vector of training labels. Y[i] is the label for X[i], and each y[i] is
an integer in the range 0 <= Y[i] < C. This parameter is optional; if it
is not passed then we only return scores, and if it is passed then we
instead return the loss and gradients.
- reg: Regularization strength.
- grad: flag to or NOT to return the loss gradients
Returns:
- loss: Loss (data loss and regularization loss) for this batch of training
samples.
- grads: Dictionary mapping parameter names to gradients of those parameters
with respect to the loss function; has the same keys as self.params.
"""
N, D = X.shape
# Compute the forward pass
fc1 = X.dot(W1) + b1 # fully connected
X2 = np.maximum(0, fc1) # ReLU
F = X2.dot(W2) + b2 # fully connected
# Compute the loss
F = F - np.max(F, axis=1).reshape(-1,1)
expF = np.exp(F)
softmax = expF/np.sum(expF, axis=1).reshape(-1,1)
loss = np.sum(-np.log(softmax[range(N),Y])) / N + reg * (np.sum(W2 * W2) + np.sum( W1 * W1 ))
if grad == True: # loss gradient is optionals
# Backward pass: compute gradients
softmax[np.arange(N) ,Y] -= 1
softmax /= N
# W2 gradient
dW2 = X2.T.dot(softmax) # [HxN] * [NxC] = [HxC]
# b2 gradient
db2 = softmax.sum(axis=0)
# W1 gradient
dW1 = softmax.dot(W2.T) # [NxC] * [CxH] = [NxH]
dfc1 = dW1 * (fc1>0) # [NxH] . [NxH] = [NxH]
dW1 = X.T.dot(dfc1) # [DxN] * [NxH] = [DxH]
# b1 gradient
db1 = dfc1.sum(axis=0)
# regularization gradient
dW1 += reg * 2 * W1
dW2 += reg * 2 * W2
dW = np.hstack((dW1.flatten(), db1, dW2.flatten(), db2))
return (loss, dW)
return loss
def train(self, X, Y, reg=1e-3, gtol=1e-5, maxiter=1000, verbose=False):
"""
Train this neural network using stochastic gradient descent.
Inputs:
- X: A numpy array of shape (N, D) giving training data.
- y: A numpy array f shape (N,) giving training labels; y[i] = c means that
X[i] has label c, where 0 <= c < C.
- X_val: A numpy array of shape (N_val, D) giving validation data.
- y_val: A numpy array of shape (N_val,) giving validation labels.
- reg: Scalar giving regularization strength.
- num_iters: Number of steps to take when optimizing.
- verbose: boolean; if true print progress during optimization.
"""
self.params["loss_history"] = []
D, H = self.params['W1'].shape
H, C = self.params['W2'].shape
def obj(x):
W1 = x[0: D*H].reshape(D,H)
b1 = x[D*H: D*H+H]
W2 = x[D*H+H: D*H+H+(H*C)].reshape(H,C)
b2 = x[D*H+H+(H*C):]
loss = self.loss(W1, b1, W2, b2, X, Y, reg=reg, grad=True)
self.params["loss_history"].append(loss[0])
if verbose == True:
print(loss[0])
return loss
x0 = np.hstack((self.params['W1'].flatten(),
self.params['b1'],
self.params['W2'].flatten(),
self.params['b2']))
res = minimize(obj, x0, method='L-BFGS-B', jac=True, options={'gtol': gtol, 'maxiter': maxiter, 'disp': True})
self.params["W1"] = res.x[0: D*H].reshape(D,H)
self.params["b1"] = res.x[D*H: D*H+H]
self.params["W2"] = res.x[D*H+H: D*H+H+(H*C)].reshape(H,C)
self.params["b2"] = res.x[D*H+H+(H*C):]
def predict(self, X):
"""
Use the trained weights of this two-layer network to predict labels for
data points. For each data point we predict scores for each of the C
classes, and assign each data point to the class with the highest score.
Inputs:
- X: A numpy array of shape (N, D) giving N D-dimensional data points to
classify.
Returns:
- Y_pred: A numpy array of shape (N,) giving predicted labels for each of
the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
to have class c, where 0 <= c < C.
"""
# Unpack variables from the params dictionary
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
# Compute the forward pass
fc1 = X.dot(W1) + b1 # fully connected
X2 = np.maximum(0, fc1) # ReLU
scores = X2.dot(W2) + b2 # fully connected
y_pred = np.argmax( scores, axis=1)
return y_pred
Example 1: Breast Cancer Wisconsin¶
https://archive.ics.uci.edu/dataset/17/breast+cancer+wisconsin+diagnostic
Load training and test dataset:
data = np.loadtxt("./datasets/breast_cancer/wdbc.data", delimiter=",", dtype=str)
X = np.float32(data[:, 2:12]) # 10 dimensions
# Diagnosis (M = malignant, B = benign)
Y = np.zeros(X.shape[0], dtype=np.int32)
Y[np.where(data[:,1]=='M')] = 1
Y[np.where(data[:,1]=='B')] = 0
print("Dimension numbers :", X.shape[1])
print("Number of data :", X.shape[0])
print("Labels :", np.unique(Y))
# For the NN
input_size = X.shape[1]
num_classes = len(np.unique(Y))
Dimension numbers : 10
Number of data : 569
Labels : [0 1]
Split the data into train and test datasets:
X_train = X[0:400, :]
Y_train = Y[0:400]
X_test = X[401:, :]
Y_test = Y[401:]
num_test = X_test.shape[0]
These are some hyperparameters that we need to tune. A new parameter called: hidden_size descirbes how many neurons in the hidden layer.
hidden_size = 100 # Try 20, 25, 50, 100
reg = 1 # Try 1.0 or 0.1 or 0.01
hidden_size = 20
net = TwoLayerNet(input_size, hidden_size, num_classes)
stats = net.train(X_train, Y_train, reg=1.0, gtol=0.001, maxiter=100, verbose=False)
# Predict on the validation set
train_acc = (net.predict(X_train) == Y_train).mean()
print('Training accuracy : ', train_acc)
# Predict on the validation set
val_acc = (net.predict(X_test) == Y_test).mean()
print('Validation accuracy : ', val_acc)
Training accuracy : 0.8725
Validation accuracy : 0.8630952380952381
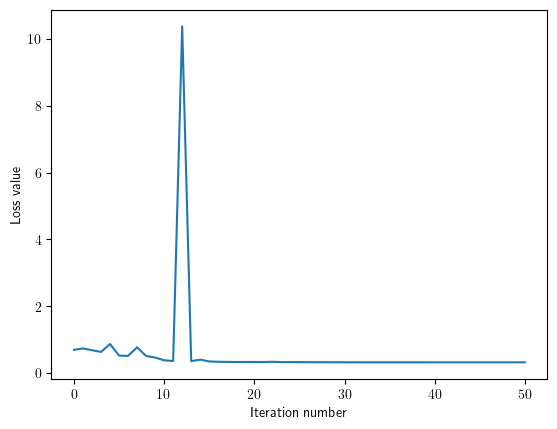
plt.plot(net.params["loss_history"])
plt.xlabel('Iteration number')
plt.ylabel('Loss value')
plt.show()
Example 2: Heart Failure Prediction¶
https://www.kaggle.com/datasets/andrewmvd/heart-failure-clinical-data
data = np.loadtxt("./datasets/heart_failure/heart_failure_clinical_records_dataset.csv", delimiter=",", skiprows=1, dtype=str)
X = np.float32(data[:, 0:12]) # 12 dimensions
Y = np.int32(data[:, -1])
print("Dimension numbers :", X.shape[1])
print("Number of data :", X.shape[0])
print("Labels :", np.unique(Y))
# For the NN
input_size = X.shape[1]
num_classes = len(np.unique(Y))
Dimension numbers : 12
Number of data : 299
Labels : [0 1]
Standardization:
We need to do standarization because tha numerical data of all features are in different order of magnitude!

means = np.mean(X, axis=0)
stds = np.std(X, axis=0)
X_train = (X[0:200, :] - means) / stds
Y_train = Y[0:200]
X_test = (X[201:, :] - means) / stds
Y_test = Y[201:]
num_test = X_test.shape[0]
hidden_size = 20
net = TwoLayerNet(input_size, hidden_size, num_classes, std=1)
stats = net.train(X_train, Y_train, reg=0.01, gtol=1e-5, maxiter=100, verbose=False)
# Predict on the validation set
train_acc = (net.predict(X_train) == Y_train).mean()
print('Training accuracy : ', train_acc)
# Predict on the validation set
val_acc = (net.predict(X_test) == Y_test).mean()
print('Validation accuracy : ', val_acc)
Training accuracy : 0.88
Validation accuracy : 0.9081632653061225
plt.plot(net.params["loss_history"])
plt.xlabel('Iteration number')
plt.ylabel('Loss value')
plt.show()

Example 3: Handwritten Digits¶
This dataset is publicly available and can be downloaded from this link.
Let us start with the train dataset:
data = np.loadtxt("./datasets/handwritten_digits/optdigits.tra", delimiter=",", dtype=int)
X_train = np.int32(data[:, 0:-1])
Y_train = np.int32(data[:, -1])
print("Dimension numbers :", X_train.shape[1])
print("Number of data :", X_train.shape[0])
print("Labels :", np.unique(Y_train))
# For the NN
input_size = X_train.shape[1]
num_classes = len(np.unique(Y_train))
Dimension numbers : 64
Number of data : 3823
Labels : [0 1 2 3 4 5 6 7 8 9]
data = np.loadtxt("./datasets/handwritten_digits/optdigits.tes", delimiter=",", dtype=int)
X_test = np.int32(data[:, 0:-1])
Y_test = np.int32(data[:, -1])
print("Dimension numbers :", X_test.shape[1])
print("Number of data :", X_test.shape[0])
print("Labels :", np.unique(Y_test))
Dimension numbers : 64
Number of data : 1797
Labels : [0 1 2 3 4 5 6 7 8 9]
for i in range(100):
X_train_ = X_train[i,:].reshape(8, 8)
X_train_ = np.abs(255.0 - 255.0 / 16.0 * X_train_)
plt.subplot(20, 10, i + 1)
# Rescale the weights to be between 0 and 255
plt.imshow(X_train_.astype('uint8'), cmap='Greys')
plt.axis('off')

Now, let us setup and then train the neural network.
hidden_size = 100
net = TwoLayerNet(input_size, hidden_size, num_classes)
stats = net.train(X_train, Y_train, reg=0.1, gtol=1e-3, maxiter=100, verbose=False)
Next, we check the accuray for training and test dataset.
# Predict on the validation set
train_acc = (net.predict(X_train) == Y_train).mean()
print('Training accuracy : ', train_acc)
# Predict on the test set
test_acc = (net.predict(X_test) == Y_test).mean()
print('Test accuracy : ', test_acc)
Training accuracy : 0.9670415903740518
Test accuracy : 0.9404563160823595
plt.plot(net.params["loss_history"])
plt.xlabel('Iteration number')
plt.ylabel('Loss value')
plt.show()

