Collection of Solvers

Author: Auralius Manurung, ME, Universitas Pertamina, auralius.manurung@ieee.org

For an ODE: $\dot{y}(t,y) = f(t,y)$ The solution takes a form of $y(t)=\dots$

Contents

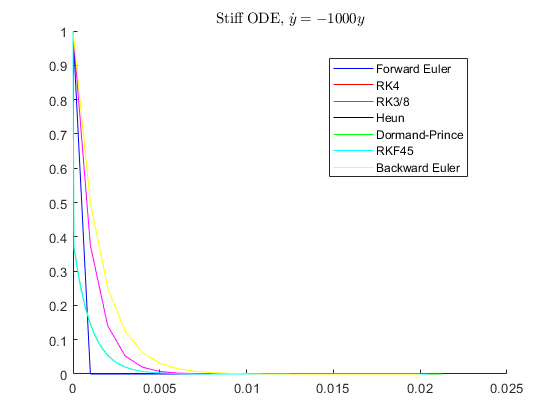
Test 1 : A very stiff system

disp('Running Test 1 ...')

[ta, ya] = feuler(@myode1, 1, 0, 0.02, 0.001);
[tb, yb] = rk4(@myode1, 1, 0, 0.02, 0.001);
[tc, yc] = rk38(@myode1, 1, 0, 0.02, 0.001);
[td, yd] = heun(@myode1, 1, 0, 0.02, 0.001);
[te, ye] = dormandprince(@myode1, 1, 0, 0.02, 0.001, 1e-9);
[tf, yf] = rkf45(@myode1, 1, 0, 0.02, 0.001, 1e-9);
[tg, yg] = beuler(@myode1, 1, 0, 0.02, 0.001);

figure
hold on
plot(ta, ya, 'b')
plot(tb, yb, 'r')
plot(tc, yc, 'm')
plot(td, yd, 'k')
plot(te, ye, 'g')
plot(tf, yf, 'c')
plot(tg, yg, 'y')
legend('Forward Euler', 'RK4', 'RK3/8', 'Heun', 'Dormand-Prince', ...
       'RKF45', 'Backward Euler', 'Location', 'Best');
title('Stiff ODE, $\dot{y} = -1000y$', 'interpreter', 'latex');

Running Test 1 ...

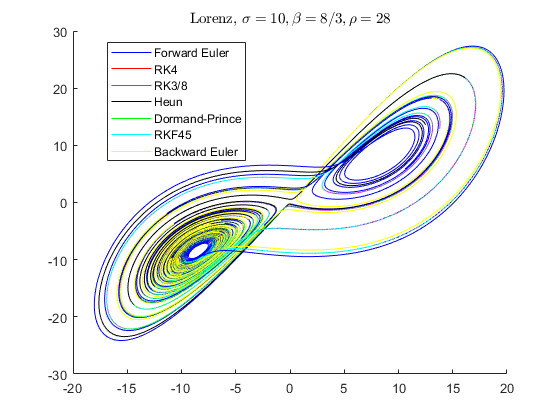
Test 2 : Lorenz dynamics

disp('Running Test 2 ...')

[ta, ya] = feuler(@myode2, [1 1 1]', 0, 20, 0.001);
[tb, yb] = rk4(@myode2, [1 1 1]', 0, 20, 0.001);
[tc, yc] = rk38(@myode2, [1 1 1]', 0, 20, 0.001);
[td, yd] = heun(@myode2, [1 1 1]', 0, 20, 0.001);
[te, ye] = dormandprince(@myode2, [1 1 1], 0, 20, 0.001, 1e-9);
[tf, yf] = rkf45(@myode2, [1 1 1], 0, 20, 0.001,  1e-9);
[tg, yg] = beuler(@myode2, [1 1 1]', 0, 20, 0.001);

figure
hold on
plot3(ya(1,:), ya(2,:), ya(3,:), 'b');
plot3(yb(1,:), yb(2,:), yb(3,:), 'r');
plot3(yc(1,:), yc(2,:), yc(3,:), 'm');
plot3(yd(1,:), yd(2,:), yd(3,:), 'k');
plot3(ye(1,:), ye(2,:), ye(3,:), 'g');
plot3(yf(1,:), yf(2,:), yf(3,:), 'c');
plot3(yg(1,:), yg(2,:), yg(3,:), 'y');
legend('Forward Euler', 'RK4', 'RK3/8', 'Heun', 'Dormand-Prince', ...
       'RKF45', 'Backward Euler', 'Location', 'Best');
title('Lorenz, $\sigma = 10, \beta = 8/3, \rho = 28$', 'interpreter', 'latex');

Running Test 2 ...

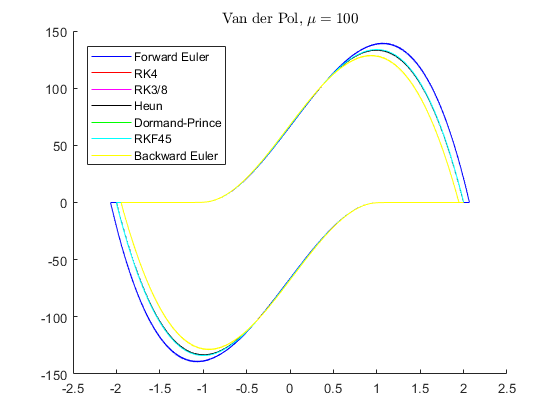
Test 3 : Van der Pol oscillator

disp('Running Test 3 ...')

[ta, ya] = feuler(@myode3, [2 0]', 0, 1000, 0.001);
[tb, yb] = rk4(@myode3, [2 0]', 0, 1000, 0.001);
[tc, yc] = rk38(@myode3, [2 0]', 0, 1000, 0.001);
[td, yd] = heun(@myode3, [2 0]', 0, 1000, 0.001);
[te, ye] = dormandprince(@myode3, [2 0]', 0, 1000, 0.001, 1e-9);
[tf, yf] = rkf45(@myode3, [2 0]', 0, 1000, 0.001,  1e-9);
[tg, yg] = beuler(@myode3, [2 0]', 0, 1000, 0.001);

figure
hold on
plot(ya(1,:), ya(2,:), 'b');
plot(yb(1,:), yb(2,:), 'r');
plot(yc(1,:), yc(2,:), 'm');
plot(yd(1,:), yd(2,:), 'k');
plot(ye(1,:), ye(2,:), 'g');
plot(yf(1,:), yf(2,:), 'c');
plot(yg(1,:), yg(2,:), 'y');
legend('Forward Euler', 'RK4', 'RK3/8', 'Heun', 'Dormand-Prince', ...
       'RKF45', 'Backward Euler', 'Location', 'Best');
title('Van der Pol, $\mu = 100$', 'interpreter', 'latex');

Running Test 3 ...

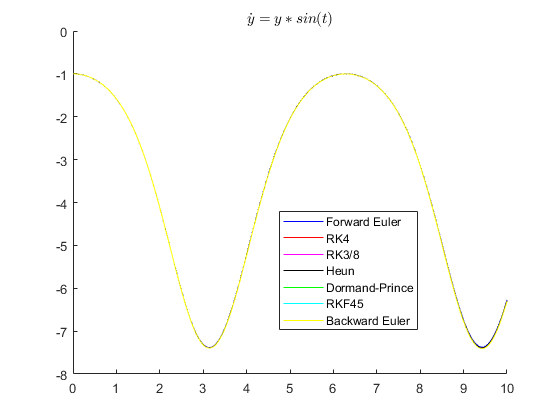
Test 4 : A simple sine wave

disp('Running Test 4 ...')

[ta, ya] = feuler(@myode4, -1, 0, 10, 0.001);
[tb, yb] = rk4(@myode4, -1, 0, 10, 0.001);
[tc, yc] = rk38(@myode4, -1, 0, 10, 0.001);
[td, yd] = heun(@myode4, -1, 0, 10, 0.001);
[te, ye] = dormandprince(@myode4, -1, 0, 10, 0.001, 1e-9);
[tf, yf] = rkf45(@myode4, -1, 0, 10, 0.001, 1e-9);
[tg, yg] = beuler(@myode4, -1, 0, 10, 0.001);

figure
hold on
plot(ta, ya, 'b');
plot(tb, yb, 'r');
plot(tc, yc, 'm');
plot(td, yd, 'k');
plot(te, ye, 'g');
plot(tf, yf, 'c');
plot(tg, yg, 'y')
legend('Forward Euler', 'RK4', 'RK3/8', 'Heun', 'Dormand-Prince', ...
       'RKF45', 'Backward Euler', 'Location', 'Best');
title('$\dot{y} = y * sin(t)$', 'interpreter', 'latex');

Running Test 4 ...

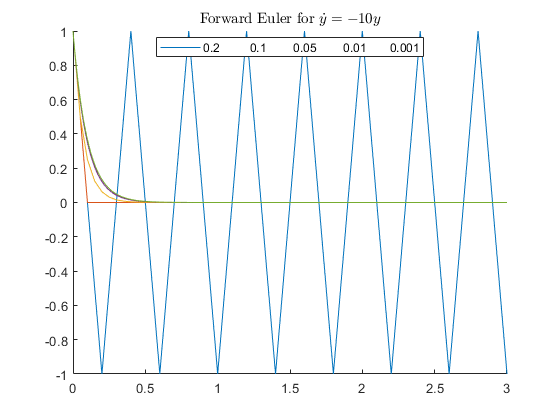
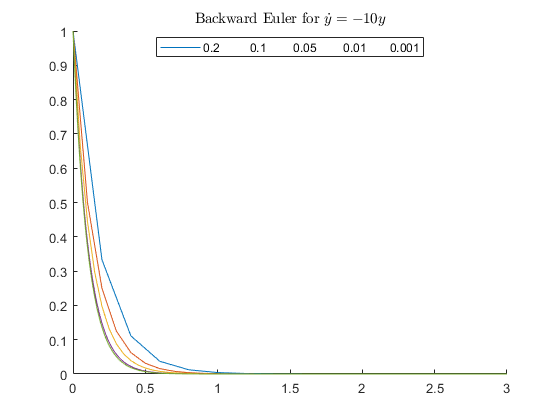
Test 5 : A special test to compare Forward Euler and Backward Euler

The test is taken from https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/node3.html Forward Euler becomes unstable when 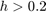$h>0.2$. Backward Euler is unconditionally stable.

disp('Running Test 5 ...')

h = [0.2 0.1 0.05 0.01 0.001];

figure
hold on
for k = 1 : length(h)
    [t, y] = feuler(@myode5, 1, 0, 3, h(k));
    plot(t, y)
end
legend(num2str(h), 'Location', 'best');
title ('Forward Euler for $\dot{y} = -10y$', 'interpreter', 'latex')

figure
hold on
for k = 1 : length(h)
    [t, y] = beuler(@myode5, 1, 0, 3, h(k));
    plot(t, y)
end
legend(num2str(h), 'Location', 'best');
title ('Backward Euler for $\dot{y} = -10y$', 'interpreter', 'latex')

Running Test 5 ...

Some ODES that we can use to test the solvers

% ------ A very stiff ODE ------
function ydot = myode1(t,y)
ydot = -1000*y;
end

% ------ Lorenz dynamics ------
function ydot = myode2(t,y)
sigma = 10;
beta = 8/3;
rho = 28;
ydot = [sigma * (y(2) - y(1));
    y(1) * (rho - y(3)) - y(2);
    y(1) * y(2) - beta * y(3)];
end

% ------ Van der Pol oscillator ------
function ydot = myode3(t,y)
Mu = 100;
ydot = [y(2); Mu*(1-y(1)^2)*y(2)-y(1)];
end

% ------ A simple sine wave ------
function ydot = myode4(t,y)
ydot = y*sin(t);
end

% ------ An ODE wih a decaying solution ------
function ydot = myode5(t,y)
ydot = -10*y;
end
% --------------------------------------------

Forward Euler method

function [t, y] = feuler(odefun, ...  % The ODE function
                         y0, ...      % Initial states
                         ts, ...      % Start time
                         tf, ...      % End time
                         h)           % Step time
t = ts:h:tf;
y = zeros(length(y0),length(t));
y(:,1) = y0;
for k = 2 : length(t)
    ydot = odefun(t(k), y(:,k-1));
    y(:,k) = y(:,k-1)+ydot.*h;
end
end

Fourth oder Runge-Kutta
function [t, y] = rk4(odefun, ...  % The ODE function
                      y0, ...      % Initial states
                      ts, ...      % Start time
                      tf, ...      % End time
                      h)           % Step time
t = ts:h:tf;
y = zeros(length(y0),length(t));
y(:,1) = y0;

for k = 2 : length(t)
    yn = y(:,k-1);
    tn = t(k-1);
    k1 = h * odefun(tn, yn);
    k2 = h * odefun(tn + h / 2 , yn + k1 / 2);
    k3 = h * odefun(tn + h / 2, yn + k2 / 2);
    k4 = h * odefun(tn + h, yn + k3);

    y(:,k) = yn + k1 / 6 + k2 / 3 + k3 / 3 + k4 / 6;
end
end

Runge-Kutta 3/8 method
function [t, y] = rk38(odefun, ...  % The ODE function
                       y0, ...      % Initial states
                       ts, ...      % Start time
                       tf, ...      % End time
                       h)           % Step time
t = ts:h:tf;
y = zeros(length(y0),length(t));
y(:,1) = y0;

for k = 2 : length(t)
    yn = y(:,k-1);
    tn = t(k-1);
    k1 = h * odefun(tn, yn);
    k2 = h * odefun(tn + h / 3, yn + k1 / 3);
    k3 = h * odefun(tn + h * 2 / 3, yn + - k1 / 3 + k2);
    k4 = h * odefun(tn + h, yn + k1 - k2 + k3);

    y(:,k) = yn + 1 / 8 * k1 + 3 / 8 * k2 + 3 / 8 * k3 + 1 / 8 * k4;
end
end

Heun's method
function [t, y] = heun(odefun, ...  % The ODE function
                       y0, ...      % Initial states
                       ts, ...      % Start time
                       tf, ...      % End time
                       h)           % Step time
t = ts:h:tf;
y = zeros(length(y0),length(t));
y(:,1) = y0;

for k = 2 : length(t)
    yn = y(:,k-1);
    tn = t(k-1);
    k1 = h * odefun(tn, yn);
    k2 = h * odefun(tn + h, yn + k1);

    y(:,k) = yn + 1 / 2 * k1 + 1 / 2 * k2;
end
end

Dormand-prince method
This is an adaptive method with variable time step
function [t, y] = dormandprince(odefun, ...   % The ODE function
                                y0, ...       % Initial states
                                ts, ...       % Start time
                                tf, ...       % End time
                                h, ...        % Step time
                                TOL)          % Local error tollerance
y(:,1) = y0;

k = 2;
t = ts;
while t < tf
    yn = y(:,k-1);
    tn = t(k-1);
    k1 = h * odefun(tn, yn);
    k2 = h * odefun(tn+h/5, yn+k1/5);
    k3 = h * odefun(tn+h*3/10, yn+k1*3/40 + k2*9/40);
    k4 = h * odefun(tn+h*4/5, yn + k1*44/45 - k2*56/15 + k3*32/9);
    k5 = h * odefun(tn+h*8/9, yn + k1*19372/6561 - k2*25360/2187 + ...
                    k3*64448/6561 - k4*212/729);
    k6 = h * odefun(tn+h, yn + k1*9017/3168 - k2*355/33 + ...
                    k3*46732/5247 + k4*49/176 - k5*5103/18656);
    k7 = h * odefun(tn+h, yn + k1*35/384 + k3*500/1113 + k4*125/192 - ...
                    k5*2187/6784 + k6*11/84);

    Y = yn + 35/384*k1 + 500/1113*k3 + 125/192*k4 - 2187/6784*k5 + ...
        11/84*k6;
    Z = yn + 5179/57600*k1 + 7571/16695*k3 + 393/640*k4 - ...
        92097/339200*k5 + 187/2100*k6 + 1/40*k7;

    E = norm(Y-Z); % local error estimation
    h = 0.9 * h * (TOL/E)^(1/5);

    y(:,k) = Y;
    t(k) = t(k-1) + h;
    k = k + 1;
end
end

Runge-Kutta-Fehlberg method (RKF45)
This is an adaptive method with variable time step.
function [t, y] = rkf45(odefun, ...   % The ODE function
                        y0, ...       % Initial states
                        ts, ...       % Start time
                        tf, ...       % End time
                        h, ...        % Step time
                        TOL)          % Local error tollerance
y(:,1) = y0;

k = 2;
t = ts;
while t < tf
    yn = y(:,k-1);
    tn = t(k-1);
    k1 = h * odefun(tn, yn);
    k2 = h * odefun(tn+h/4, yn+k1/4);
    k3 = h * odefun(tn+h*3/8, yn+k1*3/32 + k2*9/32);
    k4 = h * odefun(tn+h*12/13, yn + k1*1932/2197 - k2*7200/2197 + ...
                    k3*7296/2197);
    k5 = h * odefun(tn+h, yn + k1*439/216 - 8*k2 + k3*3680/513 - ...
                    k4*845/4104);
    k6 = h * odefun(tn+h/2, yn - k1*8/27 + k2*2 - k3*3544/2565 + ...
                    k4*1859/4104 - k5*11/40);

    Y = yn + 25/216*k1 + 1408/2565*k3 + 2197/4104*k4 - 1/5*k5;
    Z = yn + 16/135*k1 + 6656/12825*k3 + 28561/56430*k4 - 9/50*k5 + ...
        2/55*k6;

    E = norm(Y-Z); % local error estimation
    h = 0.9 * h * (TOL/E)^(1/5);

    y(:,k) = Y;
    t(k) = t(k-1) + h;
    k = k + 1;
end
end

Backward Euler method
function [t, y] = beuler(odefun, ... % The ODE function
                         y0, ...     % Initial states
                         ts, ...     % Start time
                         tf, ...     % End time
                         h, ...      % Step time
                         TOL, ...    % Tollerance for Newton's method
                         MAX_ITER)   % Max iterations for Newton's method

if nargin < 6
    TOL = 0.0001;
    MAX_ITER = 1000;
elseif nargin < 7
    MAX_ITER = 1000;
end

t = ts:h:tf;
y = zeros(length(y0),length(t));
I = eye(length(y0));

y(:,1) = y0;

for k = 1 : length(t)-1
    y1 = y(:,k);
    F = build_F(odefun, t(k), y(:,k), y1, h);
    y2 = y1 - (I-h*Jacobian(odefun, t(k), y1)) \ F;

    n_iterations = 1;
    while (norm(y2-y1) > TOL && n_iterations < MAX_ITER)
        y1 = y2;
        F = build_F(odefun, t(k), y(:,k), y1, h);
        y2 = y1 - (I-h*Jacobian(odefun, t(k), y1)) \ F;
        n_iterations = n_iterations + 1;
    end

    y(:,k+1) = y2;
end
end

% -------------------------------------------------------------------------
% Build the equation: F = 0
% -------------------------------------------------------------------------
function F = build_F(f, t, y1, y2, h)
F = y2 - y1 - h*f(t, y2);
end

% -------------------------------------------------------------------------
% Calculate Jacobian of function f at given x
% Complex-Step Derivative Approximation (CSDA) Method
% See: https://github.com/auralius/numerical-jacobian
% -------------------------------------------------------------------------
function DF = Jacobian(f, t, x, epsilon)
if nargin < 4
    epsilon = 1e-5;
end

epsilon_inv = 1/epsilon;

nx = length(x); % Dimension of the input x;

% Do perturbation
for k = 1 : nx
    xplus = x;
    xplus(k) =  x(k) + 1i*epsilon;
    DF(:, k) = imag(f(t, xplus))  .* epsilon_inv;
end
end
% ------------------------------------------------------------------------


Published with MATLAB® R2021b